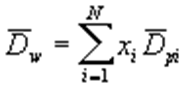- Particle technology is a term used to refer to the science and technology related to the handling and processing of particles.
- Particle technology is also often described as powder technology, particle science and powder science.
- Particles are commonly referred to as bulk solids, particulate solids and granular solids
- Today particle technology includes the study of liquid drops, emulsions and bubbles as well as solid particles.
- This course is however limited only to solid particles.
- The discipline of particle technology now includes topics as diverse as the formation of aerosols to the design of bucket elevators, crystallization to pneumatics transport, slurry filtration to silo design.
Importance
- Solids used in chemical industries are most commonly in form of particles.
- Solids in general are more difficult to handle then liquid and gases.
- In process industries solid appear in variety of forms, they may be hard and abrasive, tough and rubbery, soft and fragile, dusty and cohesive, Free flowing or sticky.
- Particulate materials, powders or bulk solids are used widely in all areas of the process industries, for example in the food processing, pharmaceutical, biotechnology, oil, chemical, mineral processing, metallurgical, detergent, power generation, paint, plastics and cosmetics industries.
- So the knowledge of their properties, handling, storage, transportation, separation and processing is important from chemical engineering point of view.
Course Content
- Introduction to the subject.
- Characterization of solid particles (size, shape and density).
- Fundamentals of solid handling (conveying and storage).
- Mixing
- Size reduction (crushing and grinding).
- Size enlargement (crystallization, pelletization, and granualization).
- Motion of particles in a fluid.
- Separation techniques
- Screening and Sieving (for solid – solid separation)
- Sedimentation and Filtration (for solid – liquid separation)
- Gas cleaning (for solid – gas separation)
Books to be consult
- Coulson & Richardson’s Chemical Engineering by J F Richardson & J H Harker with J R Backhurst. Volume 2, Fifth Edition.
- Units Operations of Chemical Engineering by Warren Lee McCabe, Julian Smith & Peter Harriott. Seventh Edition.
- Introduction to Particle Technology by Martin Rhodes. Second Edition.
1. Characterization of Solid Particle
Individual solid particles are characterized by their size, shape and density.
Size and shape are easily specified for regular particles, such as spheres and cubes, but for irregular particles ?
Why measure particle properties?
- Better control of quality of product (cement, urea, cosmetics etc)
- Better understanding of products, ingredients.
- Designing of equipment for different operations such as crushing, grinding, conveying, separation, storage etc.
Which particle properties are important to measure?
- In addition to chemical composition, the behavior of particulate materials is often dominated by the physical properties of the constituent particles.
- These can influence a wide range of material properties including, for example, reaction and dissolution rates, how easily ingredients flow and mix, or compressibility and abrasivity.
- From a manufacturing and development perspective, some of the most important physical properties to measure are:
- Particle size
- Particle shape
- Surface properties
- Mechanical properties
- Charge properties
- microstructure
1.1. Particle shape
- The shape of an individual particle is expressed in terms of the sphericity which is independent of particle size.
- Sphericity is the ratio of surface area of sphere of same volume as particle to the surface area of particle.
- So for spherical particle sphericity is equal to one.
- For non-spherical particle it is defined by:
- Dp: equivalent diameter of particle
- Sp: surface area of one particle
- vp: volume of one particle
- The equivalent diameter is sometimes defined as the diameter of a sphere of equal volume.
- For fine particles, Dp is usually taken to be the nominal size based on screen analysis or microscopic analysis.
- The surface area is found from adsorption measurements or from the pressure drop in a bed of particles.
- For many crushed materials, Sphericity is between 0.6 and 0.8. For particles rounded by abrasion, their sphericity may be as high as 0.95.
- Exercise: Determine the sphericity of a particle of surface area 15 mm2 and volume 2 mm3.

1.2. Particle size
- By far the most important physical property of particulate samples is particle size.
- Particle size measurement is routinely carried out across a wide range of industries and is often a critical parameter in the manufacturing of many products.
- Particle size has a direct influence on material properties such as:
- Reactivity or dissolution rate e.g. catalysts, tablets
- Stability in suspension e.g. sediments, paints
- Efficacy of delivery e.g. asthma inhalers
- Texture and feel e.g. food ingredients
- Appearance e.g. powder coatings and inks
- Flowability and handling e.g. granules
- Viscosity e.g. nasal sprays
- Packing density and porosity e.g. ceramics.
- In general "diameter" may be specified for any equidimensional particles (e.g. emulsions or bubbles).
- Most of the solid particles used in industries are not equidimensional, therefore cannot be specified by a single dimension i.e. “diameter”.
- In order to simplify the measurement process, it is often convenient to define the particle size using the concept of equivalent spheres.
- In this case the particle size is defined by the diameter of an equivalent sphere having the same property as the actual particle such as volume or mass for example.

- The equivalent sphere concept works very well for regular shaped particles.
- However, it may not always be appropriate for irregular shaped particles, such as needles or plates, where the size in at least one dimension can differ significantly from that of the other dimensions.
- Such particles are often characterized by the second longest major dimension. For example needle like particles, Dp would refer to the thickness of the particle, not their length.
- Units used for particle size depend on the size of particles.
- Coarse particles: inches or millimetres
- Fine particles: screen size
- Very fine particles: micrometers or nanometers
- Ultra fine particles: surface area per unit mass, m2/g
1.3 Mixed particle sizes and size analysis
- In a sample of uniform particles of diameter Dp, the total volume of the particles is m/ρp, where m = mass of the sample, ρp = density. Since the volume of one particle is vp, the total number of particle in the sample is:

- The total surface area of the particles is:

To apply the above two equations to mixtures of particles having various size and densities, the mixture is sorted into fractions, each of constant density and approximately constant size.
- Each fraction can then be weighed, or the individual particles in it can be counted or measured by any of the number of methods.
- Information from such a particle size analysis is tabulated to show the mass fraction in each size increment as a function of average particle size. The analysis tabulated in this way is called differential analysis.
- A second way to present the information is through a cumulative analysis obtained by adding, consecutively, the individual increments, starting with that containing the smallest particles, and tabulating or plotting the cumulative sums against the maximum particle diameter in the increment.
- Differential Analysis

- Mass Quantities of sample of particles

- Mass fractions from data in previous figure.
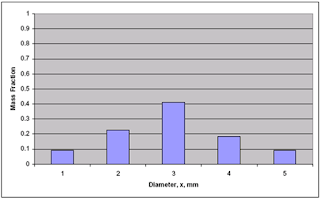
- Cumulative mass fraction plot of data from previous figure.

1.4. Specific surface of mixture
- If the particle density ρp and spericity Φs are known, the surface area of particles in each fraction can be calculated and added to give the specific surface, Aw (The total surface area of the unit mass of particles):

- Where xi = mass fraction in a given increment, Dpi = average diameter (taken as arithmetic average of the smallest and largest particle diameters in increment).
1.5. Average particle size
- The average particle size for a mixture of particles is defined in several different ways.
- Volume surface mean diameter Ds:

If number of particle Ni in each fraction is known, instead of mass fraction xi, then:
- Arithmetic mean diameter: NT = number of particles in the entire sample

- Mass mean diameter:
Volume mean diameter:

- For sample consisting of uniform particles these average diameters are, of course, all the same. For mixture containing particle of various sizes, however, the several average diameters may differ widely from one another.
1.6. Number of particles in mixture
- The volume of any particle is proportional to its "diameter" cubed.
a = volume shape factor Assuming that a is independent of size, then:
1.7 Screen analysis

- Testing sieves are made of woven wire screens.
- Openings are square.
- Screens are identified by Mesh No.
- Mesh No. is the numbers of opening per linear inch.
Area of opening in any screen = 2 x Area of opening in next smaller screen.
Mesh dimension of any screen = 1.41 x Mesh dimension of next smaller screen.
Standard screens are used to measure the size (and size distribution) of particles in the size range between about 3 and 0.0015in (76mm and 38m m).
Testing sieves are made of woven wire screens, the mesh and dimensions of which are carefully standardized.
The openings are square.
Each screen is identified in mesh per inch, e.g. 10mesh, Dpi = 1/10 = 0.1in.
The actual openings are however smaller than those corresponding to the mesh number, because of thickness of wire.
The area of the openings in any one screen in the series is exactly twice to that of the openings in the next smaller screen. The ratio of the actual mesh dimension of any screen to that of the next smaller screen is =1.41.
For close sizing, intermediate screen are available, each of which has a mesh dimension = 1.189 times that of next smaller standard screen.
Analysis using standard screen: Screens are arranged serially in a stack, with the smallest mesh at the bottom and the largest at the top. Materials are loaded at top and then shacked for a period of time (e.g. 20 minutes).
Any particle that passed the finest screen are caught in the pan at the bottom of stack.
The particles retained of each screen are removed, weighed and masses of individual screen increments are converted into mass fraction of total sample.
Any particle that passed the finest screen are caught in the pan at the bottom of stack.


- The results of screen analysis are tabulated to show the mass fraction of each screen increment as a function of the mesh size range of the increment.
- The notation 14/20 means “through 14 mesh and on 20 mesh”.
- Typical screen analysis is given in next slide.
- First column: mesh size,
- second column: width of opening of screen,
- third column: mass fraction of total sample that is retained on that screen xi (where i is the number starting from the bottom of the stack),
- fourth column: averaged particle size Dpi (since the particle on any screen are passed immediately by the screen ahead of it, the averaged of these two screen are needed to specify the averaged size in that increment).
- Fifth column: cumulative fraction smaller than Dpi
Exercise